Is an algorithm that yields a sequence of pseudo-randomized numbers calculated with a discontinuous piecewise linear equation. The method represents one of the oldest and best-known pseudorandom number generator algorithms.
The theory behind them is relatively easy to understand, and they are easily implemented and fast, especially on computer hardware which can provide modular arithmetic by storage-bit truncation.
The generator is defined by recurrence relation:
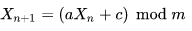
where X is the sequence of pseudorandom values, and
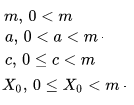
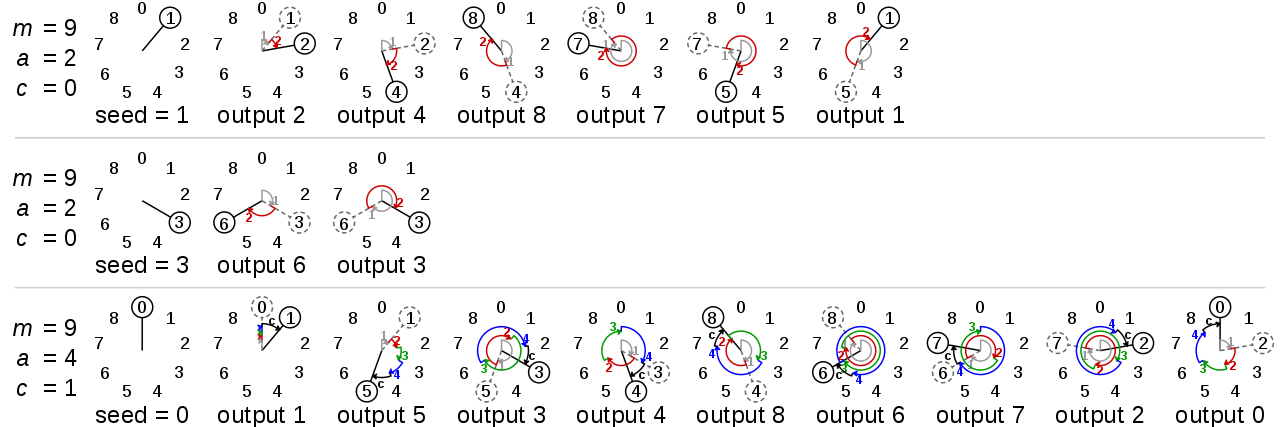
Two modulo-9 LCGs show how different parameters lead to different cycle lengths. Each row shows the state evolving until it repeats. The top row shows a generator with m = 9, a = 2, c = 0, and a seed of 1, which produces a cycle of length 6. The second row is the same generator with a seed of 3, which produces a cycle of length 2. Using a = 4 and c = 1 (bottom row) gives a cycle length of 9 with any seed in [0, 8].
